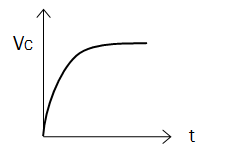
Step Response
Step Response of RC Circuits
What happens if we excite an RC circuit with Vs at t=0?
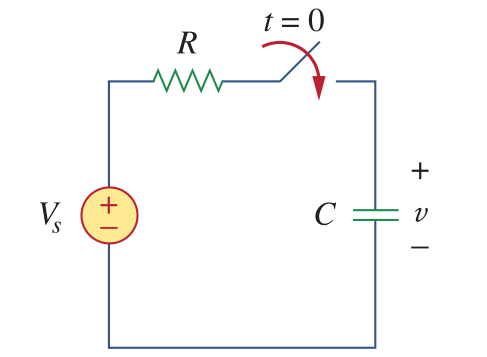
when t=0
\(i_c = V_s/R\)
for t>0
\(i_c = (V_s-V_c)/R\)
\(i_c = C \dfrac{dV_c}{dt}\)
Then;
\(C \dfrac{dV_c}{dt} = (V_s-V_c)/R\)
which can be represented as:
\(\dfrac{dV_c}{dt} = \dfrac{V_s-V_c}{RC}\)
\(\dfrac{dV_c}{V_c-V_s} = -\dfrac{dt}{RC}\)
integrating both sides and taking exponentials:
\(V_c(t)=V_s + (V_o - V_s)e^{-t/RC}\)
where \(V_0\) is the initial voltage of the capacitor.
If the initial voltage of the capacitor is zero then:
\(V_c(t)=V_s (1-e^{-t/RC})\)