RC Circuits
First-Order Circuits
Consider a circuit with resistor and capacitor as shown below.
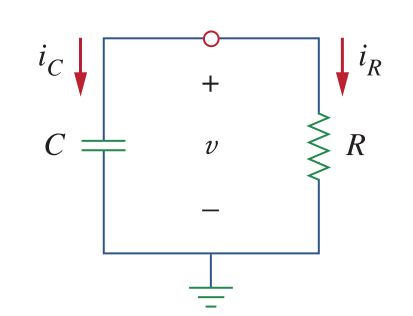
At t=0, the capacitor voltage is \(V_o\). Applying KCL at the node:
\(i_c + i_R = 0\)
\(C \dfrac{dv}{dt} + \dfrac{v}{R} = 0\)
\(\dfrac{dv}{dt} = - \dfrac{v}{RC} \)
which is a first order differential equation.
\(\dfrac{dv}{v} = - \dfrac{1}{RC}dt\)
Integrating both sides:
\( ln (v) = -\dfrac{t}{RC} + ln (A)\)
or:
\( ln (\dfrac{v}{A}) = -\dfrac{t}{RC}\)
taking exponential power on each sides:
\( v(t) = Ae^{-\dfrac{t}{RC}}\)
As we know the initial voltage is \(V_0\). Thus:
\( v(t) = V_oe^{-\dfrac{t}{RC}}\)
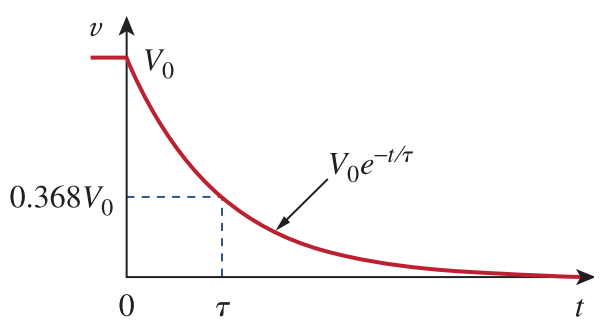
Thus, the voltage response of a RC circuit is an exponential decay of voltage. The time constant of the circuit is given as:
\(\tau=RC\)
The unit of the time constant is in seconds.
Thus, the equation above becomes:
\( v(t) = V_oe^{-\dfrac{t}{\tau}}\)
, which is presented in the figure below:
Exercise:
If the initial voltage of the capacitor is 60 V, then determine Vc, Vx, io.
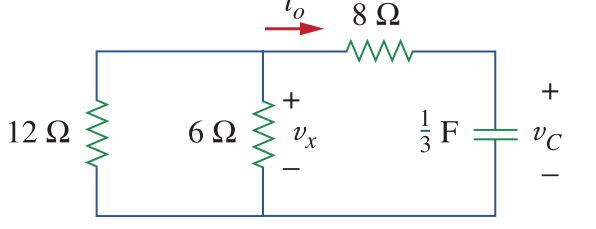
60, 20, -5