EE281 - Electric Circuits

Nodal Analysis

In the nodal analysis, node voltages are calculated by solving the Kirchhoff's Current Law (KCL) equations obtained from each node.

Method includes the following steps:

Choose a reference node (ground)
Label node voltages
Write KCL equations for each node except the ground node.

(For reference check Nodal Analysis e-book).

1-Choose a reference node (or ground node)

It is best to choose ground node as the node interconnects the most branches.
The ground node is usually at the bottom of circuit.
Label ground with one of the symbols below:

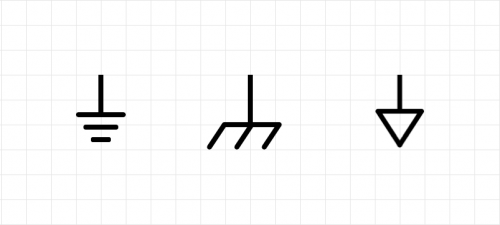
2-Assign node voltages

Give label to each node except the reference node.

3- Write KCL equations

write KCL equations (the most practical way is to use negative sign for the currents entering to the node), positive sign for currents exiting from the node).
After defining KCL for each node, the equations can be put in matrix form and the problem can be solved.

4-Solve

Methods for solving system of linear equations:

Elimination Method : Simplest but not really scalable to more complex equations
Row reduction: A systematical way of elimination, can be applied to more complex cases, but it's time consuming.
Cramer's Rule (example): Practical for up to 3x3 matrices.
Inverse Matrix Method: Scalable to even the most complex cases, but you'll need a calculator or computer.

Example 1:

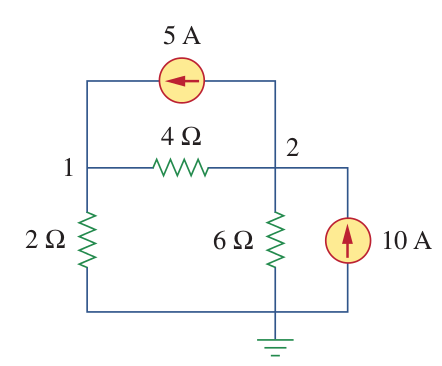
Calculate the node voltages for the following circuit¹:

¹. Alexander&Sadiku, 2012, pg84. ↩

Answer: V1= 40/3 V, V2= 20 V

Matrix Equations

Example:

Apply the nodal analysis in the following circuit: This is some text.

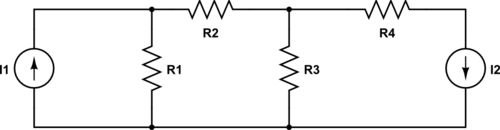
Define the bottom node as the reference node
Apply KCL for each node:

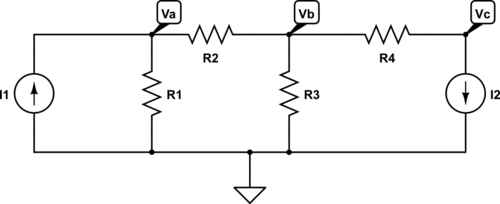
Node a:

$-I_1 + \frac{V_a}{R_1} + \frac{V_a-V_b}{R_2} = 0$

Node b:

$\frac{V_b-V_a}{R_2} + \frac{V_b}{R_3} + \frac{V_b-V_c}{R_4} = 0$

Node c:

$\frac{V_c-V_b}{R_4} + I_2 = 0$

Then everything can be put into matrix form:

$\begin{bmatrix} \frac{1}{R_1}+\frac{1}{R_2} & -\frac{1}{R_2} & 0 \\ -\frac{1}{R_2} & \frac{1}{R_2}+ \frac{1}{R_3}+\frac{1}{R_4} & -\frac{1}{R_4} \\ 0 & -\frac{1}{R_4} & \frac{1}{R_4} \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \\ \end{bmatrix} + \begin{bmatrix} -I_1 \\ 0 \\ I_2 \\ \end{bmatrix} =0$

which is equivalent to

$\begin{bmatrix} \frac{1}{R_1}+\frac{1}{R_2} & -\frac{1}{R_2} & 0 \\ -\frac{1}{R_2} & \frac{1}{R_2}+ \frac{1}{R_3}+\frac{1}{R_4} & -\frac{1}{R_4} \\ 0 & -\frac{1}{R_4} & \frac{1}{R_4} \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \\ \end{bmatrix} = \begin{bmatrix} I_1 \\ 0 \\ -I_2 \\ \end{bmatrix}$

For convenience instead of resistance, conductance can also be used:

$G = \frac{1}{R}$

Thus, the equation becomes:

$\begin{bmatrix} G_1+G_2 & -G_2 & 0 \\ -G_2 & G_2+ G_3+G_4 & -G_4 \\ 0 & -G_4 & G_4 \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \\ \end{bmatrix} = \begin{bmatrix} I_1 \\ 0 \\ -I_2 \\ \end{bmatrix}$

Note that, this is a classic matrix equation:

$AX = B$

This equation can be solved as:

$X = A^{-1}B$

where $A^{-1}$ is the inverse of matrix A. In order to get the inverse of a matrix it has to be a square matrix. Furthermore, due to KCL applied A matrix in an electric circuit will be symmetrical.