Mutual Flux

Suppose two coils are placed near each other, as in:

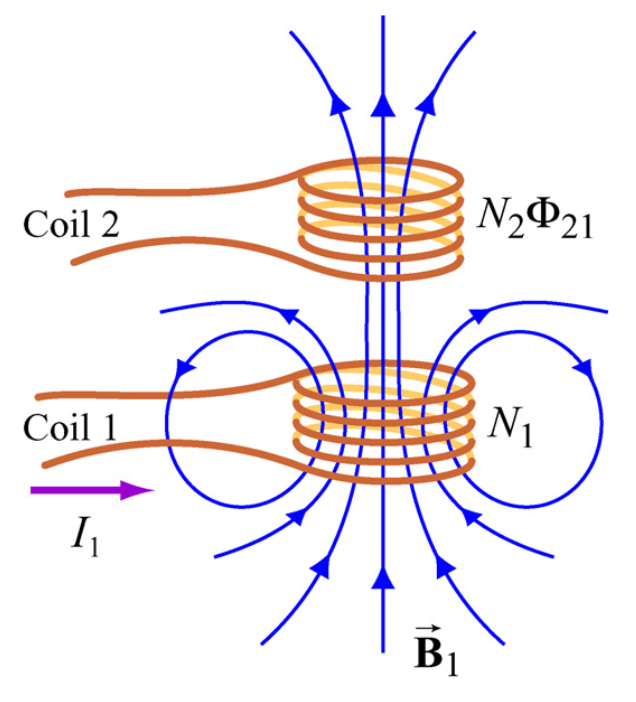
The first coil is excited with sinusoidal excitation and creates a magnetic field that also links Coil#2. Let (\Phi_{21}) is the magnetic flux that links coil #2. As, the I is varying with time, there will be an induced emf in Coil#2:

$$V{21} = - N_2 \frac{d \Phi{21}}{dt}$$ The flux linkage in Coil#2 is proportional to current in Coil#1. Thus, let's define the mutual inductance ((M_{21})) as:

$$N2 \frac{d\Phi{21}}{dt} = M_{21} \frac{dI_1}{dt}$$ Mutual inductance can also be defined as:

$$M{21}=\frac{N_2 \Phi{21}}{I_1}$$ Special Case: For linear system (e.g. air)

$$\Phi_{21} = \frac{N_1 I_1}{\mathrm{R}}$$ where (\mathrm{R}) is the reluctance for the flux path. Mutual inductance becomes:

$$M = \frac{N_1 N_2}{\mathrm{R}}$$