Magnetic Circuits
Magnetic circuits are analogous to electric circuits:
| Circuit | Water | Electric | Magnetic | |||
|---|---|---|---|---|---|---|
| Excitation | Force | |||||
| $$ | ||||||
| N | ||||||
| $$ | ||||||
| EMF | ||||||
| $$ | ||||||
| V | ||||||
| $$ | ||||||
| MMF ( | ||||||
| $$ | ||||||
| NI | ||||||
| $$ | ||||||
| ) | ||||||
| $$ | ||||||
| A | ||||||
| $$ | ||||||
| Pressure, | ||||||
| $$ | ||||||
| \vec{P} | ||||||
| $$ | ||||||
| $$ | ||||||
| N/m^2 | ||||||
| $$ | ||||||
| Electric Field, | ||||||
| $$ | ||||||
| \vec{E} | ||||||
| $$ | ||||||
| $$ | ||||||
| V/m | ||||||
| $$ | ||||||
| Magnetic Field, | ||||||
| $$ | ||||||
| \vec{H} | ||||||
| $$ | ||||||
| $$ | ||||||
| A/m | ||||||
| $$ | ||||||
| Outcome | Water Flow | |||||
| $$ | ||||||
| m^3/s | ||||||
| $$ | ||||||
| Current, | ||||||
| $$ | ||||||
| I | ||||||
| $$ | ||||||
| $$ | ||||||
| A | ||||||
| $$ | ||||||
| Flux, | ||||||
| $$ | ||||||
| \Phi | ||||||
| $$ | ||||||
| $$ | ||||||
| Wb | ||||||
| $$ | ||||||
| Flow Density | ||||||
| $$ | ||||||
| m/s | ||||||
| $$ | ||||||
| Current Density, | ||||||
| $$ | ||||||
| \vec{J} | ||||||
| $$ | ||||||
| $$ | ||||||
| A/m^2 | ||||||
| $$ | ||||||
| Flux Density, | ||||||
| $$ | ||||||
| \vec{B} | ||||||
| $$ | ||||||
| $$ | ||||||
| Wb/m^2, T | ||||||
| $$ | ||||||
| Flow Limiter | Resistance | Resistance, | ||||
| $$ | ||||||
| R | ||||||
| $$ | ||||||
| $$ | ||||||
| \Omega | ||||||
| $$ | ||||||
| Reluctance, | ||||||
| $$ | ||||||
| \mathcal{R} | ||||||
| $$ | ||||||
| $$ | ||||||
| A/Wb | ||||||
| $$ | ||||||
| Conductivity, | ||||||
| $$ | ||||||
| \sigma | ||||||
| $$ | ||||||
| $$ | ||||||
| S/m | ||||||
| $$ | ||||||
| Permeability, | ||||||
| $$ | ||||||
| \mu | ||||||
| $$ | ||||||
| $$ | ||||||
| H/m | ||||||
| $$ | ||||||
| Resistivity, | ||||||
| $$ | ||||||
| \rho | ||||||
| $$ | ||||||
| $$ | ||||||
| \Omega.m | ||||||
| $$ | ||||||
| Reluctivity, | ||||||
| $$ | ||||||
| m/H | ||||||
| $$ | ||||||
Basic Materials:
| Electric Circuits | Magnetic Circuits |
|---|---|
| Conductors: Copper, Aluminum | Ferromagnets: Iron, Electrical Steel |
| Insulators: Air, Plastic | Non-magnetics: |
| Copper, Water (Diamagnetic) | |
| Air, Aluminum (Paramagnetic) |
! In electric circuits, copper is
$$ 10^{22}
$$ more conducting than air, thus we can say air is an insulating material. However, in magnetic circuits magnetic materials are just 4000-5000 times more "conducting", thus there is not a real insulator in magnetic circuits, and air-gaps should be considered in calculations.
Magnetic Field and Magnetic Force:
When electric charges are in motion(e.g. current conducting through a wire), they experience some forces apart from the electrostatic forces, which are called magnetic forces.
Flux, $$\Phi$$, (Wb=Volt.s)
A magnetic field characterized by lines of force called flux lines.

Flux Density, B ($$Wb/m^2 = T$$)
It's the density of magnetic flux per unit area. If the magnetic flux is uniform:
$$B=\frac{\Phi}{A} \quad (Wb/m^2)$$
Magneto-motive Force, MMF ($$A.t$$)
It is the excitation force in a magnetic circuit. The unit of MMF is Ampere turns(
$$ A.t
$$ ), or just Amperes (
$$ A
$$ ).
Magnetic Circuits & Maxwell Equations
$$\begin{align} \textrm{Gauss' Law}\quad &\nabla \cdot \vec{E} = \frac{\rho}{\varepsilon_0}\ \textrm{Gauss' Law ($\vec{B}$ Fields)} \quad &\nabla \cdot \vec{B} = 0\ \textrm{Faraday's Law} \quad &\nabla \times\quad \vec{E} = - \frac{\partial \vec{B}}{\partial t}\ \textrm{Ampere's Law} \quad &\nabla \times \vec{B} = \mu_0 \vec{J} + \mu_0\varepsilon_0\frac{\partial \vec{E}}{\partial t} \end{align}$$ In quasi-static fields:
1. Ampere's Law
The line integral of the magnetic field around a closed path is equal to the surface integral of current density of the same loop (or to total Ampere.turns).
$$\oint_C {\vec{H}.d\vec{\ell}} = \bigcirc!!!!!!!!!\iint_S \vec{J}.\vec{n}dA$ = \sum I_n$$ Magnetic field intensity(H) is independent of the material properties!
Calculate the magnetic field around a current-carrying conductor (as a function of the radius,r):
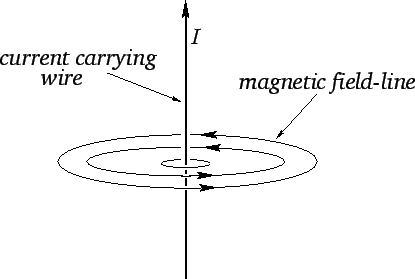
For r, H is constant due to symmetry:
$$\oint_C {\vec{H}.d\vec{\ell}} = \sum I_n$$$$H \oint_C {d\vec{\ell}} = H 2\pi r = I \rightarrow H=\frac{I}{2\pi r}$$ Calculate the MMF in the circuit below:

Assume, H is constant inside the magnetic core.
$$MMF= \oint_C {\vec{H}.d\vec{\ell}} = \sum I_n =NI$$
2. Gauss Law (for Magnetism)
In a specific region of magnetic field, the number of flux lines entering and leaving the region is zero.
$$\nabla \cdot {B} =0$$ or in integral form, net flux lines in a closed surface is zero
$$\bigcirc!!!!!!!!!\iint_S \vec{B}.\vec{n}dA = 0$$ Practical meaning: There are no net magnetic flux sources. (If you break a magnet into two smaller magnets, you don't have one south-pole and one north-pole magnet. Each magnet will have its own north and south pole) You can watch Sheldon Cooper on magnetic di-poles. You can also watch Richard Feynman on magnetic forces.
Ohm's Law (for a magnetic circuit)
In electric circuits, we have:
$$V=IR$$ In magnetic circuits(Magneto-motive-force:
$$ \mathcal{F}
$$ ):
$$\mathcal{F} = \Phi \mathcal{R}$$ **Magnetic Reluctance (
$$ \mathcal{R}
$$ )** Similar to the calculation of electric resistance (instead of conductvity use permeability)
$$\mathcal{R} = \frac{l}{\mu A}$$ where
$$ l
$$ is the length of the material,
$$ A
$$ is the cross-sectional area and **
$$ \mu
$$ is the magnetic permeability**.
Flux Density - Magnetic Field Relation ($$B=\mu H$$)
Magnetic flux density is found dividing the magnetic flux by area:
$$B=\frac{\Phi}{A}$$ MMF is the
$$ H
$$ multiplied by length (
$$ l
$$ ), (or similarly in the integral form):
$$\mathcal{F} = H l$$ Thus,
$$ \mathcal{F} = \Phi \mathcal{R}
$$ can be written as:
$$Hl = BA \frac{l}{\mu A}$$ which gives:
$$\vec{B} = \mu \vec{H}$$ It is similar to the relation between current density, electric field and conductivity (i.e.
$$ \vec{J}=\rho \vec{E}
$$ ).
Magnetic Permeability
The magnetic permeability of free space(vacuum) is:
$$\mu_0 = 4 \pi 10^{-7} \quad H/m$$ Instead of defining exact permeability of materials, it is common practice to define permeability relative to permeability of vacuum, which is called relative permeability (
$$ \mu_r
$$ ).
$$\mu = \mu_o . \mu_r$$ For example typical relative permeability of iron is around 4000 (
$$ \mu_r=4000
$$ ), which means iron condurc magnetic fields 4000 times easier compared to vacuum. The exact permeability of iron is:
$$\mu_{iron} = 4000\mu_0 = 16\pi10^{-4} H/m$$ You can also come across with Permeance, which is the inverse of permeability(
$$ \frac{1}{\mu}
$$ ).
(Permeability = conductivity, permeance = resistivity).
Exercise:
- Calculate the reluctance of the iron core in terms of $$ \mu_0 $$ , assuming $$ \mu_r=4000 $$ , $$ l=500 mm $$ , $$ A_c=2500mm^2 $$ .

!! Don't forget to convert into SI units (e.g. mm to m)
$$\mathcal{R}=\frac{l}{\mu0\mu_rA}$$$$\mathcal{R{core}}=\frac{0.5}{\mu_0.4000.2500.10^{-6}}=\frac{0.05}{\mu_0}$$
- Now, calculate the reluctance again with the air-gap added as below. Relative permeability of air is 1 ( $$ \mu_r=1 $$ ), and assume the air-gap is 3 mm.
We can think the circuit as two series resistances connected together.

Core reluctance
$$ \mathcal{R}_{core}
$$ almost stays same:
$$\mathcal{R}_{core}=\frac{0.499}{\mu_0.4000.2500.10^{-6}} \sim \frac{0.05}{\mu_0}$$ Air-gap reluctance (
$$ \mu_r=1
$$ ):
$$\mathcal{R}_{ag}=\frac{0.003}{\mu_0.2500.10^{-6}}= \frac{1.2}{\mu_0}$$ Total reluctance becomes:
$$\mathcal{R}{eq}=\mathcal{R}{core}+\mathcal{R}{ag}$$$$\mathcal{R}{eq}=\frac{0.05}{\mu_0}+\frac{1.2}{\mu_0}=\frac{1.25}{\mu_0}$$ We increased the equivalent reluctance 25 times, by adding just a small air-gap. Air-gap reluctances dominates the magnetic circuit, so it is usually acceptable to neglect core reluctance by assuming
$$ \mu_r = \infty
$$ .
- Calculate and compare the flux density (B) in the core, for each case assuming $$ N_{turns}=7 $$ and $$ i=5A $$ .
The equivalent circuit diagrams are shown above. Let's calculate the total flux in each case:
$$\mathcal{F} = \Phi \mathcal{R}$$$$\Phi = \frac{NI}{\mathcal{R}{eq}}$$$$\Phi{without-gap} = \frac{NI \mu0}{0.05}$$$$\Phi{with-gap} = \frac{NI \mu_0}{1.25}$$ putting in the numbers:
$$\Phi{without-gap} \sim 0.88 mWb$$$$\Phi{with-gap} \sim 0.035 mWb$$ Flux density can be found by dividing the magnetic flux by area.
$$B=\frac{\Phi}{Area}$$$$B{without-gap} =\frac{0.88mWb}{2500.10^{-6} m^2}=0.352 \; T$$$$\Phi{with-gap} \frac{0.035mWb}{2500.10^{-6} m^2}=0.014 \; T$$ Increasing reluctance (by adding air-gap_ reduces the magnetic flux.